概要
コンソールで動作する簡易なAI付きオセロゲームをC++で書いたので、簡単に説明する。
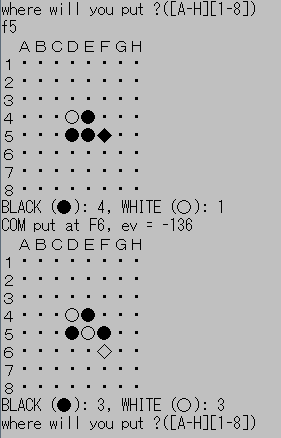
本稿で解説するオセロのソースコードは以下から取得できる。
ライセンスは CDDL 1.0 なので、自由に改変して再配布してOKだぞ。
解説
クラス
盤面を表す Boad クラスだけ。
盤面状態を保持し、初期化、盤面表示、着手可能判定、着手処理、着手を元に戻す、盤面評価などのメンバ関数を持つ
盤面データ構造
(通常サイズの)オセロ盤面サイズは 8x8 なので、盤面の状態は、単純には int board[8][8] のような2次元配列で表現できるが、
余分な添字計算を省くために1次元配列を用いるのが普通である。
※ 配列ではなくビットボードを用いる方法もあるが、プログラムが高度になるので本プログラムでは採用しなかった。
着手可能判定や着手処理において、盤面をスキャンして石を挟んでいるかどうかを判定する必要がある。
そのとき、盤面の端に到達したかどうかを座標チェックではなく、状態で簡単にチェックできると処理が高速になる。
そのために導入されるのが「壁(WALL)」である。壁は番人と呼ばれ、広く使われるテクニックである。
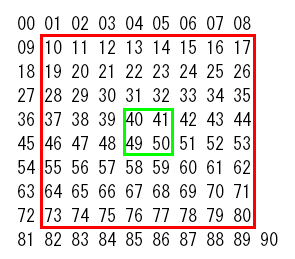
上図が1次元配列の各要素を盤面に対応付けたものである。赤枠で囲っているところが盤面に対応し、それ以外は壁である。
右下のマス目(H8)から右下方向に移動した場合に対応するため、添字 90 の要素があることに注意されたい。
緑枠で囲っている部分は初期状態で石が置いてある位置を表している。
盤面配列は uchar m_board[ARY_SIZE]; で宣言している。
uchar は unsigned char の typedef である。
ARY_SIZE は壁(番人)を含めた1次元配列サイズで、Borad クラス内で enum 定数として定義されている。
石を挟んでいるかどうかの判定のための盤面スキャンは8方向に対して行われる。 それぞれの方向には定数が Borad クラス内で enum 定数として定義されている。
盤面配列各要素の値は、空(EMPTY)、黒(BLACK)、白(WHITE)、壁(WALL) のいずれかの値をとる。 これらも、Borad クラス内で enum 定数として定義されている。
enum {
BD_WIDTH = 8, // 盤面の縦・横サイズ
ARY_WD = BD_WIDTH + 1, // 盤面配列の横サイズ
ARY_HT = BD_WIDTH + 2, // 盤面配列の縦サイズ
ARY_SIZE = (ARY_WD * ARY_HT + 1), // 盤面配列サイズ
ORI_UL = -(ARY_WD + 1), // 左上方向
ORI_U = -ARY_WD, // 上方向
ORI_UR = -(ARY_WD - 1), // 右上方向
ORI_L = -1, // 左方向
ORI_R = 1, // 右上方向
ORI_DL = ARY_WD - 1, // 左下方向
ORI_D = ARY_WD, // 下方向
ORI_DR = ARY_WD + 1, // 右下方向
EMPTY = 0, // 空
BLACK = 1, // 黒
WHITE = 2, // 白
WALL = 255, // 壁(番人)
};
座標変換関数
int xyToIx(int x, int y) は、x, y 座標(範囲は [1, 8])を盤面配列インデックスに変換する。
int IxToX(int ix), int IxToY(int ix) は上記の逆の変換を行う関数である。
盤面の状態を変えたり、盤面の状態を返すものではないので、 static 関数にしている。
盤面初期化
init() 関数で盤面を初期化。
最初に盤面配列(m_board)を全て壁(WALL)埋め、ついで for文で y, x を回して空(EMPTY)で埋める。
最後に中央の4箇所に黒・白石を配置する
盤面表示
盤面表示は Boad::print() 関数で行っている。
for文で x, y を回して盤面の石を表示。
上、左部の英数字も表示。
着手可能判定
オセロはタテ・ヨコ・ナナメの8方向に対して、相手の石を自分の石で挟める場合のみ着手可能であるので、 指定箇所に着手可能かどうかを判定するには、8方向に対して、相手の石が続き、自分の石があるかどうかをチェックするとよい。
bool Board::canPutBlackSub(int ix, int ori) const は ix 位置に黒石を打った場合に ori 方向に白石を挟めるかをチェックする関数。
判定コードは以下のように記述できる。
// 黒石を ix に置いた場合、ori 方向に石が返るか判定
bool Board::canPutBlackSub(int ix, int ori) const
{
if( m_board[ix += ori] != WHITE )
return false; // 次の位置が白石でなければリターン
while( m_board[ix += ori] == WHITE ) {} // 白石が続く間移動
return m_board[ix] == BLACK; // 黒石があれば、挟んだことになる
}
上記コードで、盤面の端に来たことをチェックしていないことに注目して欲しい。 盤面の外には壁があるので、石の色を調べるだけでよいのだ。番人のテクニックによりコードが簡潔に記述できている。
bool Board::canPutBlack(int ix) const は canPutBlackSub() を8方向について呼び出し、ix 位置に打てるかどうかをチェックする関数。
着手処理
int Board::putBlack(int ix) は指定位置に黒石を打ち、挟まれた白石を黒に返る関数だ。
処理は、vector<int> v; を引数に指定し、Board::putBlack(int ix, vector
int Board::putBlack(int ix, vector<int> &v) ば ix 位置に黒石を置き、挟まれた白石を黒に変える。 その時、返した位置を vector<int> &v に保存する。これは後で出てくる undoPutBlack() 関数のための情報。 返した白石の総数と、打った位置も vector<int> &v に保存する。
着手処理の undo
void Board::undoPutBlack(vector<int> &v) は、putBlack() で保存した情報を元に、返した白石を元に戻し、
打った黒石の場所を空に戻す関数。
この後説明する、ミニマックス探索・アルファベータ探索で、先読みした局面を元に戻す時に使用される。
評価関数
int Board::eval() は黒番の局面の評価値を計算する評価関数。
評価関数とは、局面がどの程度有利かを計算する関数のことである。
チェスではひとつのポーンの価値を100点として計算するのが普通。(モンテカルロ法の)囲碁では勝つ確率を計算するのが普通である。
本プログラムでは、1石勝ちを+100として計算している。
どのように評価関数を定義するかは非常に難しい問題である。 本プログラムは簡易的なものであり、準確定石数と着手可能箇所数のみを考慮した極めて簡単な評価関数を定義している。(なので、かなり弱い)
ミニマックス探索
「ミニマックス探索」の説明は大変なので、ぐぐって調べてください。
アルファベータ探索
「アルファベータ探索」の説明は大変なので、ぐぐって調べてください。